定义:
递归(英语:Recursion),在数学和计算机科学中是指在函数的定义中使用函数自身的方法,在计算机科学中还额外指一种通过重复将问题分解为同类的子问题而解决问题的方法。
引入:
递归的基本思想是某个函数直接或者间接地调用自身,这样原问题的求解就转换为了许多性质相同但是规模更小的子问题。求解时只需要关注如何把原问题划分成符合条件的子问题,而不需要过分关注这个子问题是如何被解决的。
递归代码最重要的两个特征:结束条件和自我调用。自我调用是在解决子问题,而结束条件定义了最简子问题的答案。
int func(传入数值) {
if (终止条件) return 最小子问题解;
return func(缩小规模);
}
递归的缺点
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。而栈不是无限大的,当递归层数过多时,就会造成 栈溢出 的后果。
显然有时候递归处理是高效的,比如归并排序;有时候是低效的,因为堆栈会消耗额外空间,而简单的递推不会消耗空间
递归的优化
主页面:搜索优化 和 记忆化搜索
比较初级的递归实现可能递归次数太多,容易超时。这时需要对递归进行优化。
数数小木块
在墙角堆放着一堆完全相同的正方体小木块,如下图所示:
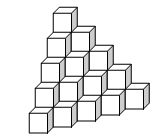
因为木块堆得实在是太有规律了,你只要知道它的层数就可以计算所有木块的数量了。
输入
只有一个整数 n ,表示这堆小木块的层数,已知 1≤n≤100 。
输出
只有一个整数,表示这堆小木块的总数量。
样例
输入复制
5
输出复制
35
#include<bits/stdc++.h>
using namespace std;
int num(int n){
if(n==1) return 1;
else return num(n-1)+n;
}
int main()
杨辉三角
Description
输出杨辉三角种指定位置的元素
Format
Input
输入两个正整数,n,m。m<=n,5<=n<=10。n表示指定行,m表示指定列
Output
输出一个整数,表示指定位置的元素
Samples
输入数据 1
5 3
输出数据 1
6
long long yh(int n,int m){ f(n,m)=f(n-1,m)+f(n-1,m-1)
if(m==1 || m==n) return 1;
return yh(n-1,m)+yh(n-1,m-1);
}
1、集合的划分
【题目描述】
设S是一个具有n个元素的集合,S=〈a1,a2,……,an〉,现将S划分成k个满足下列条件的子集合S1,S2,……,Sk且满足:
1.Si≠∅
2.Si∩Sj=∅ (1≤i,j≤k,i≠j)
3.S1∪S2∪S3∪…∪Sk=S
则称S1,S2,……,Sk是集合S的一个划分。
它相当于把S集合中的n个元素a1,a2,……,an放入k个(0<k≤n<30)无标号的盒子中,使得没有一个盒子为空。请你确定n个元素a1,a2,……,an放入k个无标号盒子中去的划分数S(n,k)。
【输入】
给出n和k。
【输出】
n个元素a1,a2,……,an放入k个无标号盒子中去的划分数S(n,k)。
【输入样例】
10 6
【输出样例】
22827
解析:
an 是k个子集中的一个,将 a1,a2,,,an-1 划分成 k-1 个子集,总数为s(n-1,k-1)
an 不是k个子集中的一个,则 an必须与其他元素构成一个子集。问题变成 现将a1,,,,an-1 划分成 k个子集,再将an-1 添加进去。根据乘法原理,
k*s(n-1,k)
综合两种情况,递归公式s(,k)=s(n-1,k-1)+k*s(n-1,k)
边界:
k=0 s=0
k>n s=0
k=1 或者 k=n s =1
#include<bits/stdc++.h>
using namespace std;
long long s(int n,int k){
if((n<k)|| (k==0)) return 0;
if((k==1)||(k==n) )return 1;
return s(n-1,k-1)+k* s(n-1,k);
}
int main(){
int n,k;
cin>>n>>k;
cout<<s(n,k)<<endl;
return 0;
}
记忆化递归
#include <bits/stdc++.h>
using namespace std;
long long s[40][40]; // s[i][j]:将i个球装j个盒子的情况数。
long long f(int n, int k) // 求将i个不相同的球放入j个盒子的方案数
{
if (s[n][k] > 0)
return s[n][k];
if (k > n)
return 0;
else if (k == 1)
return 1;
else
return s[n][k] = f(n - 1, k - 1) + k * f(n - 1, k);
}
int main()
{
int n, k;
cin >> n >> k;
cout << f(n, k);
return 0;
}
2数的计数
【题目描述】
我们要求找出具有下列性质数的个数(包括输入的自然数nn)。先输入一个自然数n(n≤1000)n(n≤1000),然后对此自然数按照如下方法进行处理:
不作任何处理;
在它的左边加上一个自然数,但该自然数不能超过原数的一半;
加上数后,继续按此规则进行处理,直到不能再加自然数为止。
【输入】
自然数n(n≤1000)n(n≤1000)。
【输出】
满足条件的数。
【输入样例】
6
1
【输出样例】
6
1
【提示】
【样例解释】
满足条件的数为如下所示:
6
16
26
126
36
136

递推
#include <bits/stdc++.h>
using namespace std;
long long a[1001];
int main(){
a[1]=1;
int n;
cin>>n;
for(int i=2;i<=n;i++){
a[i]=1;//不做任何处理,本身是1种
for(int j=1;j<=i/2;j++)
a[i]+=a[j];//1到i/2的和
}
cout<<a[n]<<endl;
return 0;
}
方法2:递归
(1)、定义f(n)为数n的方法数
(2)、边界条件:n=1时,只有一种方法
(3)、当n大于1时,f(n)=1+f(1)+f(2)…+f(n/2)
#include <bits/stdc++.h>
using namespace std;
int f(int n){
if (n==1) return 1;
int s=1;
for(int i=1;i<=n/2;i++){
s+=f(i);
}
return s;
}
int main()
{
int n;
cin>>n;
cout<<f(n)<<endl;
return 0;
}
方法3:记忆化递归
#include <bits/stdc++.h>
using namespace std;
int a[1001];
int f(int n){
if (n==1) return 1;
if(a[n]) return a[n];
a[n]=1;
for(int i=1;i<=n/2;i++){
a[n]+=f(i);
}
return a[n];
}
int main()
{
int n;
cin>>n;
a[1]=1;
cout<<f(n)<<endl;
return 0;
}
3、求s=a+aa+aaa+aaaa+aa...a的值
求 s=a+aa+aaa+aaaa+aa…a 的值,其中 aa 从键盘读入。比如:读入 2 ,则 s=2+22=24。再比如:读入 5 ,s=5+55+555+5555+55555=61725
输入
一个整数 a ( a1∼9 的范围内)
输出
整数 n 代表这个算式的结果
样例
输入复制
2
输出复制
24
#include<bits/stdc++.h>
using namespace std;
int f(int n,int a){
if(n==1){
return a;
}
return a+10*f(n-1,a);
}
int main(){
int n;
cin>>n;
int s=0;
for(int i=1;i<=n;i++){
s+=f(i,n);
}
cout<<s;
return 0;
}
4、土地分割
把一块mn米的土地分割成同样大的正方形,如果要求没有土地剩余,分割出的正方形土地最大边长是多少米?(最少不能少于1米1米)
如:一块6米 * 4米的土地,能够分割的最大的正方形的边长为2米。
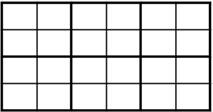
输入
两个整数m和n(m,n <= 1018)
输出
能够分割的最大正方形的边长
样例
输入复制
6 4
输出复制
2
#include<bits/stdc++.h>
using namespace std;
long long gcd(long long a,long long b){
if(a%b==0) return b;
return gcd(b,a%b);
}
int main(){
long long m,n;
cin>>m>>n;
cout<<gcd(m,n);
return 0;
}
5、买汽水
一瓶饮料n元钱,两个空瓶换一瓶,有m元最多可以喝几瓶 ?
输入
两个整数n,m(1<=n<m<=100000)
输出
最多可以喝到的瓶数
样例
输入复制
2 10
输出复制
9
#include<bits/stdc++.h>
using namespace std;
int f(int x){
if(x==1){
return 0;
}
return x/2+f(x/2+x%2);
}
int main(){
int n,m;
cin>>n>>m;
cout<<m/n+f(m/n);
return 0;
}
6、逆波兰表达式
【题目描述】
逆波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的逆波兰表示法为* + 2 3 4。本题求解逆波兰表达式的值,其中运算符包括+ - * /四个。
【输入】
输入为一行,其中运算符和运算数之间都用空格分隔,运算数是浮点数。
【输出】
输出为一行,表达式的值。
可直接用printf("%f\n", v)输出表达式的值v。
【输入样例】
* + 11.0 12.0 + 24.0 35.0
【输出样例】
1357.000000
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
char a[55];
double calculate()
{
scanf("%s",a);
if(a[0]=='+')
return calculate()+calculate();
else if(a[0]=='-')
return calculate()-calculate();
else if(a[0]=='*')
return calculate()*calculate();
else if(a[0]=='/')
return calculate()/calculate();
else
return atof(a);
}
int main()
{
printf("%f\n",calculate());
return 0;
}
atof(),是C 语言标准库中的一个字符串处理函数,功能是把字符串转换成浮点数,所使用的头文件为<stdlib.h>。
7、数根
数根是这样定义的:对于一个正整数 n ,将它的各个数位上的数字相加得到一个新数,如果这个数是一位数,我们就称之为 n 的数根,否则重复处理直到它成为一个一位数。
例如,n=34,3+4=7, 7 是一位数,所以 7 是34 的数根。
再如,n=345,3+4+5=12,1+2=3,3 是一位数,所以 3 是 345 的数根。
对于输入数字 n ,编程计算它的数根。
输入
一个正整数。(n<=10^8
输出
一个整数,代表 n 的数根。
样例
输入复制
345
输出复制
3
#include<bits/stdc++.h>
using namespace std;
int sg(int n){
if(n<10) return n;
int s=0;
while (n)
{
s+=n%10;
n/=10;
}
return sg(s);
}
int main() {
int n;
cin>>n;
cout<<sg(n);
system("pause");
return 0;
}
8、Pell数列
Pell数列a1,a2,a3,...的定义是这样的,a1=1,a2=2,...,an=2an−1+an−2(n>2)。
给出一个正整数k,要求Pell数列的第k项模上32767是多少。
【输入】
第1行是测试数据的组数 n,后面跟着 n 行输入。每组测试数据占 1 行,包括一个正整数k(1≤k<1000000)。
【输出】
n 行,每行输出对应一个输入。输出应是一个非负整数。
【输入样例】
2
1
8
【输出样例】
1
408
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define N 1000010
#define k 32767
using namespace std;
int a[N];
int f(int x)
{
if(a[x]!=0) return a[x];
if(x==1) return 1;
if(x==2) return 2;
return a[x]=(2*(f(x-1))%k+(f(x-2))%k)%k;
}
int main()
{
int n,a;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a;
cout<<f(a)<<endl;
}
return 0;
}
分解因数
【题目描述】
给出一个正整数a,要求分解成若干个正整数的乘积,即a=a1×a2×a3×...×an,并且1<a1≤a2≤a3≤...≤an,问这样的分解的种数有多少。注意到a=a也是一种分解。
【输入】
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a(1<a<32768)。
【输出】
n行,每行输出对应一个输入。输出应是一个正整数,指明满足要求的分解的种数。
【输入样例】
2
2
20
【输出样例】
1
4
#include <bits/stdc++.h>
using namespace std;
//返回数字k分解成由大于等于st的因数乘积的形式的分解方案数
int solve(int k, int st)
{
if(k == 1)//k为1表示分解结束,形成1种方案
return 1;
int ct = 0;
for(int i = st; i <= k; ++i)
{
if(k%i == 0)
ct += solve(k/i, i);//分解方案增加:将k/i分解成因数最小为i的分解方案数。
}
return ct;
}
int main()
{
int n, a;
cin >> n;
while(n--)
{
cin >> a;
cout << solve(a, 2) << endl;//分解数字a,因数大于等于2
}
return 0;
}
数组元素之和
题目描述
已知一个一维数组a[1..n](n<25),又已知一整数m。 如能使数组a中任意几个元素之和等于m,则输出YES,反之则为NO。
输入
第一行正整数n,n<25;
第二行,n个整数(不超过1000);
第三行整数m。
输出
YES或NO。
样例
输入复制
5
1 2 3 4 5
7
输出复制
YES
#include<iostream>
using namespace std;
const int max1=51;
int a[max1],n,m;
bool flag;
void sum(int n,int m)
{
if (a[n]==m) flag=true; //利用全局变量falg传递结果
else if (n==1) return; //n=1作为递归边界,不再递归下去
else //进行两种选择
{
sum(n-1,m-a[n]);
sum(n-1,m);
}
}
int main()
{
cin>>n;
for (int i=1; i<=n; ++i) cin>>a[i];
cin>>m;
flag=false;
sum(n,m);
if (flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
return 0;
}
进制转换
题目描述
上机练习6.3.6 用递归算法将一个十进制数X转换成任意进制数M(M<=16)。
输入
一行,整数X和M,X<=109,M<=16。
输出
十进制数X的M进制数。
样例
输入复制
11 2
输出复制
1011
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
char d[16] = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
int x,m;
int t(int n,int k);
int main(){
cin >> x >> m;
t(x,m);
cout << endl;
return 0;
}
int t(int n,int k) //将十进制数N转换称为K进制数
{
int r;
r = n % k; //进制转换
n /= k;
if(n != 0) //递归边界 n=0,否则继续递归。
t(n,k);
cout << d[r];
}
分数求和
【题目描述】
输入n个分数并对他们求和,并用最简形式表示。所谓最简形式是指:分子分母的最大公约数为1/1;若最终结果的分母为1,则直接用整数表示。
如:5/6、10/3均是最简形式,而3/6需要化简为1/2,3/1需要化简为3。
分子和分母均不为0,也不为负数。
【输入】
第一行是一个整数n,表示分数个数,1≤n≤10;
接下来n行,每行一个分数,用"p/q"的形式表示,不含空格,p,q均不超过10。
【输出】
输出只有一行,即最终结果的最简形式。若为分数,用"p/q"的形式表示。
【输入样例】
2
1/2
1/3
【输出样例】
5/6
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define N 1000010
using namespace std;
int a[20],b[20];
int gcd(int a,int b)
{
if(b==0)
return a;
return gcd(b,a%b);
}
int main()
{
int n;
int cnt=0;
int numerator=0,denominator=1;
int divisor;
char s[20];
cin>>n;
while(n--)
{
scanf("%d/%d",&a[cnt],&b[cnt]);
cnt++;
}
for(int i=0;i<cnt;i++)
denominator*=b[i];
for(int i=0;i<cnt;i++)
numerator=numerator+denominator*a[i]/b[i];
divisor=gcd(denominator,numerator);
denominator/=divisor;
numerator/=divisor;
if(denominator==1)
cout<<numerator<<endl;
else
cout<<numerator<<"/"<<denominator<<endl;
return 0;
}



评论区