高精度加法 +
输入两个数到变量中,然后用赋值语句求它们的和后输出 但是,我们知道,在 C++ 语言中任何数据类型都有一定表示范围. 当两个加数很大时,以前的算法显然不能求出精确解,因此我们需要寻求另一种方法 .在读小学时,我们做加法都采用竖式方法 . 这样我们方便写出两个整数相加的算法 。
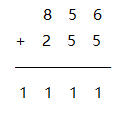
实现代码:
#include<bits/stdc++.h>
using namespace std;
//1、建立两个字符数组,三个int型数组,数组长度根据题目要求的
//数字长度设置
char a1[300],b1[300];
int a[300],b[300],c[300];//c=a+b,a是通过a1转来的 b是通过b1转来的
int main(){
int lena,lenb,lenc=1,x=0;//x表示进位的数字是几
//2、输入a1,b1
cin>>a1>>b1;
//3、将a1,b1 倒序存储到a,b中
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
lena=strlen(a1);
lenb=strlen(b1);
for(int i=0;i<=lena-1;i++)//反向存储a
a[lena-i]=a1[i]-'0';
for(int i=0;i<=lenb-1;i++)//反向存储b
b[lenb-i]=b1[i]-'0';
while(lenc<=lena || lenc<=lenb){
c[lenc]=a[lenc]+b[lenc]+x;
x=c[lenc]/10;//计算进位
c[lenc]=c[lenc]%10;//进位后,剩余多少
lenc++;
}
c[lenc]=x;//存储最高位的进位
if(c[lenc]==0)//如果最高位是0,删除最高位
lenc--;
for(int i=lenc;i>=1;i--)//反向输出c数组的值
cout<<c[i];
return 0;
}
高精度减法 -

//高精度减法:
//1、a>0&&b>0&&a>b 结果 a-b
//2、a>0&&b>0&&a<b 结果 -(b-a)
//3、a<0&&b>0 结果 -(a+b) 转换成高精度加法
//4、a>0&&b<0 结果 (a+b) 转换成高精度加法
//5、a<0&&b<0 结果(|b|-|a|)
1、将当前位置的数向减。
2、如果结果大于或等于0就直接作为当前位的答案。
3、否则将结果加10作为当前位的答案,在将高位的数-1即可。
实现代码:
#include<bits/stdc++.h>
using namespace std;
//1、建立两个字符数组,三个int型数组,数组长度根据题目要求的
//数字长度设置
char a1[300],b1[300],c1[300];
int a[300],b[300],c[300];//c=a+b,a是通过a1转来的 b是通过b1转来的
int main(){
int lena,lenb,lenc,x=0;//x表示进位的数字是几
//2、输入a1,b1
cin>>a1>>b1;
//3、比较a1和b1的大小
if((strlen(a1)<strlen(b1)) ||(strlen(a1)==strlen(b1)&&(strcmp(a1,b1)<0))){
cout<<"-";
strcpy(c1,a1);
strcpy(a1,b1);
strcpy(b1,c1);
}
//4、将a1,b1 倒序存储到a,b中
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
lena=strlen(a1);
lenb=strlen(b1);
for(int i=0;i<=lena-1;i++)//反向存储a
a[lena-i]=a1[i]-'0';
for(int i=0;i<=lenb-1;i++)//反向存储b
b[lenb-i]=b1[i]-'0';
int i=1;
while(i<=lena || i<=lenb){
if(a[i]<b[i]){
a[i]+=10;
a[i+1]--;
}
c[i]=a[i]-b[i];
i++;
}
lenc=i;
//c数组高位可能存在多个0
while(c[lenc]==0&&lenc>1) lenc--;
for(int i=lenc;i>=1;i--){
cout<<c[i];
}
}
高精度乘法 * (高精度 * 高精度)
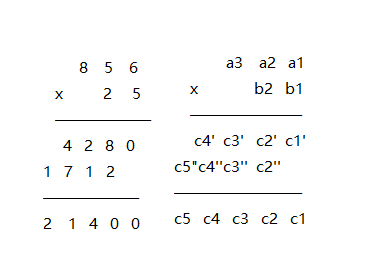
分析下标变化得到规律
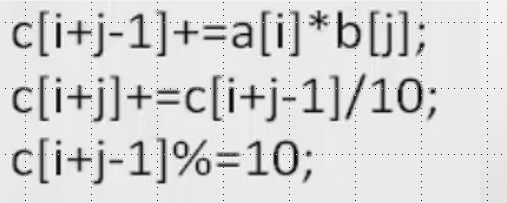
实现代码
#include<bits/stdc++.h>
using namespace std;
string s1,s2;
int a[10000],b[10000],c[10000];
int lena,lenb,lenc;
int main(){
cin>>s1>>s2;
lena=s1.size();
lenb=s2.size();
for(int i=0;i<lena;i++){
a[lena-i]=s1[i]-'0';//将字符转换为数字,并且将字符倒序转置便于计算
}
for(int i=0;i<lenb;i++){
b[lenb-i]=s2[i]-'0';
}
lenc=lena+lenb;
//核心
for(int i=1;i<=lena;i++){
for(int j=1;j<=lenb;j++){
c[i+j-1]+=a[i]*b[j];
}
}
for(int i=1;i<=lenc;i++){
c[i+1]+=c[i]/10;
c[i]=c[i]%10;
}
while(c[lenc]==0 && lenc>1) lenc--;
for(int i=lenc;i>=1;i--) cout<<c[i];
return 0;
}
高精度 * 单精度
实现代码
void mul_short(int a[], int b, int c[]) {
for (int i = 0; i < LEN - 1; ++i) {
// 直接把 a 的第 i 位数码乘以乘数,加入结果
c[i] += a[i] * b;
if (c[i] >= 10) {
// 处理进位
// c[i] / 10 即除法的商数成为进位的增量值
c[i + 1] += c[i] / 10;
// 而 c[i] % 10 即除法的余数成为在当前位留下的值
c[i] %= 10;
}
}
}
高精度除法(高精度除单精度)
做除法时,每一次的商值都在 0~9 之间,每次求得的余数连接以后的若干位得到新的被除数,继续做除法。因此,在做高精度除法时,要涉及到乘法运算和减法运算,还有移位处理。当然,为了程序简洁,可以避免高精度乘法,用 0~9 次循环减法取代得到商的值。采用按位相除法。
代码实现
#include<bits/stdc++.h>
using namespace std;
char s[10000];
int a[10000],c[10000];
long long b,x=0;
int main(){
cin>>s;
cin>>b;
a[0]=strlen(s);
for(int i=0;i<a[0];i++){
a[i+1]=s[i]-'0'; //正序存放
}
for(int i=1;i<=a[0];i++){
c[i]=(x*10+a[i])/b; // 算上上一位剩下的继续除
x=(x*10+a[i])%b; //求余数
}
int lenc=1;
while(c[lenc]==0 && lenc<a[0]){
lenc++;
}
for(int i=lenc;i<=a[0];i++){
cout<<c[i];
}
cout<<endl;
cout<<x<<endl;
return 0;
}



评论区