算法介绍
搜索,也就是对状态空间进行枚举,通过穷尽所有的可能来找到最优解,或者统计合法解的个数。
回溯算法
回溯是搜索算法中的一种控制策略。它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。
解决⼀个回溯问题,实际上就是⼀个决策树的遍历过程。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,⽆法再做选择的条件。
伪代码框架:
result = []
def backtrack(路径, 选择列表):
if 满⾜结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」
问题引入:
全排列问题
我们知道 n 个不重复的数,全排列共有 n! 个。
PS:为了简单清晰起见,我们这次讨论的全排列问题不包含重复的数字。
那么我们当时是怎么穷举全排列的呢?例如说给三个数 [1,2,3] ,你肯定
不会无规律地乱穷举,⼀般是这样:
先固定第⼀位为 1,然后第⼆位可以是 2,那么第三位只能是 3;
然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第⼀位,变成 2,然后再穷举后两位……
回溯树:
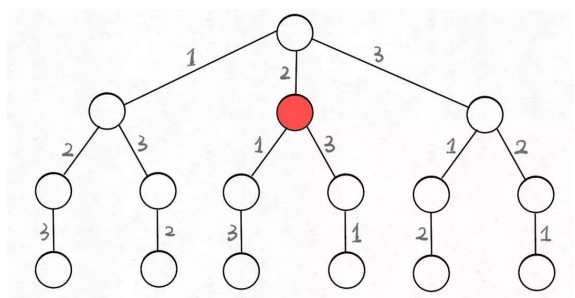
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。这棵树称为回溯算法的 「决策树」 。
在树的任意节点,都在进行决策。例如:

例如红色的节点,现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝,2号树枝不能选择,因为已经选择过了。
[2] 就是「路径」,记录你已经做过的选择;
[1,3] 就是「选择列表」,表式你当前可以做出的选择;
「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
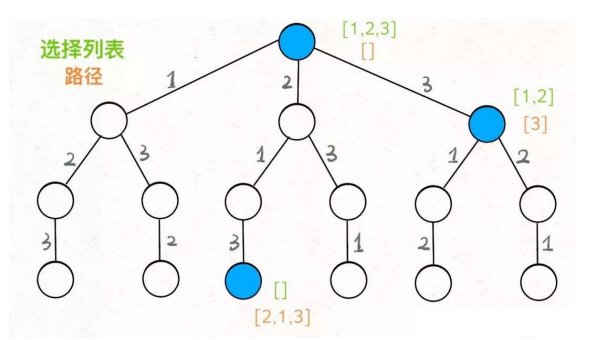
我们定义的 backtrack 函数其实就像⼀个指针,在这棵树上游走,同时要
正确维护每个节点的属性,每当⾛到树的底层,其「路径」就是⼀个全排
列。
程序框架
递归回溯法算法框架[一]
int Search(int k)
{
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果
if (到目的地) 输出解;
else Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
递归回溯法算法框架[二]
int Search(int k)
{
if (到目的地) 输出解;
else
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果;
Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
例题:
1、组合的输出
【题目描述】
排列与组合是常用的数学方法,其中组合就是从n个元素中抽出r个元素(不分顺序且r≤n),我们可以简单地将n个元素理解为自然数1,2,…,n,从中任取r个数。
现要求你用递归的方法输出所有组合。
例如n=5,r=3,所有组合为:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
【输入】
一行两个自然数n、r(1<n<21,1≤r≤n)。
【输出】
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
【输入样例】
5 3
【输出样例】
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
#include<bits/stdc++.h>
#define N 30
using namespace std;
int n,r;
int a[N];
int vis[N];
void dfs(int step)
{
int i;
if(step==r+1)
{
for(i=1;i<=r;i++)
cout<<" "<<a[i];
cout<<endl;
return;
}
for(i=a[step-1];i<=n;i++)
{
if(vis[i]==0)
{
a[step]=i;
vis[i]=1;
dfs(step+1);
vis[i]=0;
}
}
}
int main()
{
cin>>n>>r;
a[0]=1;
dfs(1);
return 0;
}



评论区