定义:
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决。
动态规划算法的基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法,只不过在计算机问题上应用比较多,比如说让你求最长递增子序列,最小编辑距离等。
要求最值,核心问题是什么呢?求解动态规划的核心问题是穷举。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值。
动态规划的穷举有点特别,因为这类问题存在「重叠子问题」,如果暴力穷举的话效率会极其低下,所以需要「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算。
而且,动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。
动态规划三要素:
重叠子问题
最优子结构
状态转移方程
斐波那契数列的数学形式就是递归的,写成代码就是这样:
int fib(int N) {
if (N == 1 || N == 2) return 1;
return fib(N - 1) + fib(N - 2);
}
这个递归算法的时间复杂度???
递归算法时间复杂度=子问题个数*解决一个子问题需要的时间
子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2n)。
解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为 O(2n),指数级别,爆炸。
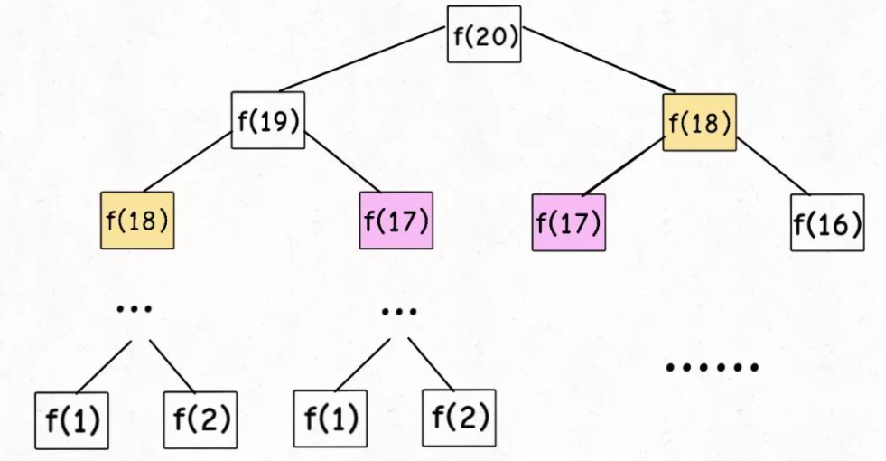
该算法存在的问题:重叠子问题
优化方向:
耗时的原因是重复计算,那么我们可以造一个「备忘录」,每次算出某个子问题的答案后别急着返回,先记到「备忘录」里再返回;每次遇到一个子问题先去「备忘录」里查一查,如果发现之前已经解决过这个问题了,直接把答案拿出来用,不要再耗时去计算。
备忘录一般使用数组
#include<bits/stdc++.h>
using namespace std;
int memo[100]={0};
int helper(int n){
if(n==1 || n==2 )return 1;
if(memo[n]!=0) return memo[n];
memo[n]=helper(n-1)+helper(n-2);
return memo[n];
}
int fib(int N){
if(N<1) return 0;
return helper(N);
}
int main(){
int n=20;
cout<<fib(n);
return 0;
}
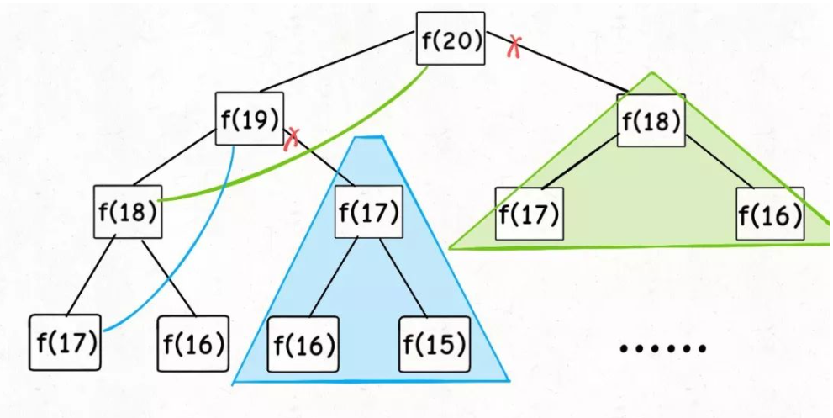
带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
本算法的时间复杂度是 O(n)
至此,带备忘录的递归解法的效率已经和迭代的动态规划一样了。实际上,这种解法和迭代的动态规划思想已经差不多,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
#include<bits/stdc++.h>
using namespace std;
int dp[100];
int fib(int N){
dp[1]=1;
dp[2]=1;
for(int i=3;i<=N;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[N];
}
int main(){
cout<<fib(6);
return 0;
}
「状态转移方程」 ——描述问题结构的数学形式
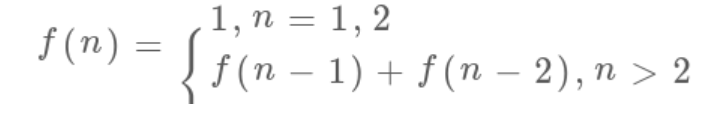
把 f(n) 想做一个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来,这就叫状态转移
动态规划问题最困难的就是写出状态转移方程
4步套路,解决动态规划问题
一、确定状态 一般是数组(一维、二维、三维)f[i]代表什么 f[x][y]代表什么
二、确定转移方程 (推导公式)
三、初始条件和边界 (初始值)
四、计算顺序 (最终结果)
例:你有三种硬币,分别面值2元,5元和7元,每种硬币都有足够多。买一本书需要27元。如何用最少的硬币组合正好付清,不需要对方找钱?求出最少用几枚硬币?最值问题
正常人第一反应思路
最少硬币组合?
优先使用大面值硬币
7+7+7+5=26
改算法——7+7+7+2+2+2=27,总共用了6枚硬币正好27元
实际正确答案:7+5+5+5+5=27,才用了5枚硬币。所以这里贪心算法是不正确的。
第一步,确定问题状态。
动态规划问题求解需要先开一个数组,并确定数组的每个元素f[i]代表什么,就是确定这个问题的状态。类似于解数学题中,设定X,Y,Z代表什么。
A、确定状态首先提取【最后一步】
最优策略必定是K枚硬币a1, a2,…, aK 面值加起来是27。
找出不影响最优策略的最后一个独立角色,这道问题中,那枚最后的硬币“aK”就是最后一步。把aK提取出来,硬币aK之前的所有硬币面值加总是27- aK
因为总体求最硬币数量最小策略,所以拼出27- aK 的硬币数也一定最少(重要设定)。

B、转化子问题。最后一步aK提出来之后,我们只要求出“最少用多少枚硬币可以拼出27- aK”就可以了。
这种与原问题内核一致,但是规模变小的问题,叫做子问题。
为简化定义,我们设状态f(X)=最少用多少枚硬币拼出总面值X。
我们目前还不知道最后的硬币aK面额多少,但它的面额一定只可能是2/5/7之一。
如果aK是2,f(27)应该是f(27-2) + 1 (加上最后这一枚面值2的硬币)
如果aK是5,f(27)应该是f(27-5) + 1 (加上最后这一枚面值5的硬币)
如果aK是7,f(27)应该是f(27-7) + 1 (加上最后这一枚面值7的硬币)
除此以外,没有其他的可能了。
至此,通过找到原问题最后一步,并将其转化为子问题。
为求面值总额27的最小的硬币组合数的状态就形成了,用以下函数表示:
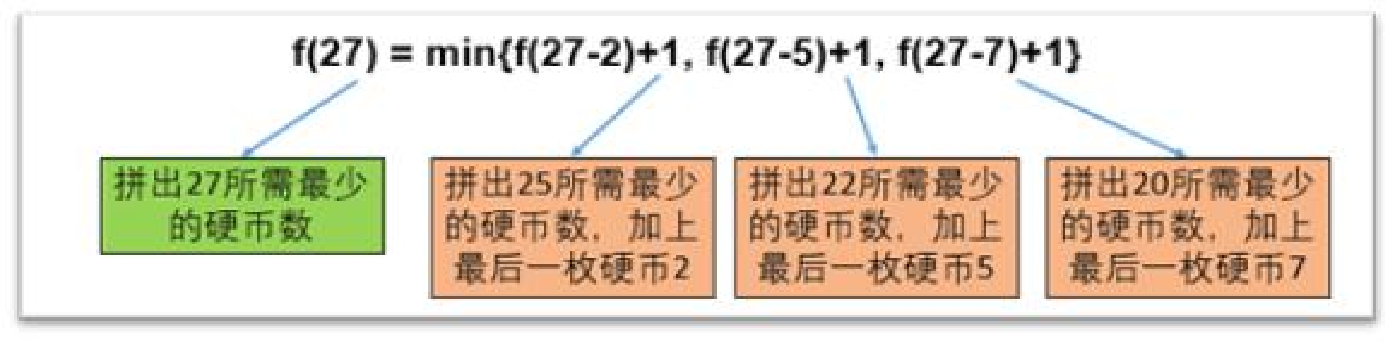
第三步,按照实际逻辑设置边界情况和初始条件。
【必做】否则即使转移方程正确也大概率无法跑通代码。
f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}的边界情况是[x-2]/[x-5]/[x-7]不能小于0(硬币面值为正),也不能高于27。
故对边界情况设定如下:
如果硬币面值不能组合出Y,就定义f[Y]=正无穷
例如f[-1]=f[-2]=…=正无穷;
f[1] =min{f[-1]+1, f[-4]+1,f[-6]+1}=正无穷,
特殊情况:本题的F[0]对应的情况为F[-2]、F[-5]、F[-7],按照上文的边界情况设定结果是正无穷。
实际上F[0]的结果是存在的(即使用0个硬币的情况下),F[0]=0。
用转移方程无法计算,但是又实际存在的情况,就必须通过手动定义。
这里手动强制定义初始条件为:F[0]=0.
第四步,确定计算顺序并计算求解
开始计算时,是从F[1]、F[2]开始呢?还是从F[27]、F[26]开始呢?
判断计算顺序正确与否的原则是:
当我们要计算F[X](等式左边,如F[10])的时候,等式右边(f[X-2], f[X-5], f[X-7]等)都是已经得到结果的状态,这个计算顺序就是OK的。
实际就是从小到大的计算方式
#include<bits/stdc++.h>
using namespace std;
int A[3]={2,5,7} ,M=27;
int f[28];
int coinChange(){
for(int i=1;i<=M;i++){
for(int j=0;j<3;j++){
if(i>=A[j] && f[i-A[j]]!=INT_MAX){
f[i]=min(f[i-A[j]]+1,f[i]);
}
}
}
if(f[M]==INT_MAX){
return -1;
}
return f[M];
}
int main(){
f[0]=0;
for(int i=1;i<=M;i++){
f[i]=INT_MAX;
}
cout<<coinChange()<<endl;
for(int i=1;i<=M;i++){
cout<<i<<":"<<f[i]<<endl;
}
return 0;
}



评论区