数论入门
质因数分解
质数是无法进行质因数分解的。
把正整数拆分成质数的幂的乘积的过程,称为整数的质因数分解
24=2×2×2×3=2^3×3^1
33=3×11=3^1×11^1
17=17=17^1
唯一分解定理
正整数的质因数分解是唯一的:
n=p_1^r_1*p_2^r_2*p_3^r_3⋯
其中p_i是质数。p_1=2,p_2=3,p_3=5,依此类推。
约数个数
这个问题可以通过质因数分解来回答。
e.g. 180=22 ×32 ×51
哪些数是它的因数呢?
根据之前的结论,这些数可以表示为:
p=2a × 3b ×5c
其中a,b,c是非负整数,满足a≤2,b≤2,c≤1.
a可取{0,1,2},共3种取法
b可取{0,1,2},共3种取法
c可取{0,1},共2种取法
(a,b,c)共有3∗3∗2=18种取法
每种取法对应了一个约数
也就是说,如果一个数n可以分解为:
n=p_1r_1 ⋅p_2r_2⋅ p_3^r_3⋯
则它的约数个数为:
d=(r_1+1)(r_2+1)(r_3+1)⋯
最大公约数
两个数n和m,它们的最大公约数是:gcd(n,m)
gcd(a,b)=gcd(b,a%b)
//代码:
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b){
if (b==0) return a;
return gcd(b,a%b);
}
int main(){
cout<<gcd(100,80);
return 0;
}
最小公倍数记作:lcm(n,m)
lcm(n,m)=n⋅m/gcd(n,m)
在计算lcm的时候,初学者往往使用下面的代码:
lcm(n,m)=n⋅m/gcd(n,m)
实际上这是不妥当的。因为n⋅m可能会爆掉int.
正确的写法是:
lcm(n,m) = n/gcd(n,m)*m
互质
如果a和b除1以外没有公因数,则称a,b互质。
只需要判断gcd(a,b)是否为1.
模的性质
a%p的值一定落在[0,p−1]之间
取模有两个很好的性质:
加法 (a+b)%p=(a%p+b%p)%p
乘法 (ab)%p=[(a%p)⋅(b%p)]%p
随时取模
在只含加法和乘法的式子中,如果最后的运算结果需要对p取模,在运算过程中取模。
只需要最后把结果对p再取模,答案就是正确的。
质数
质数(prime)又叫素数。定义为:
一个正整数p是质数,当且仅当它的约数只有1和它本身。
因此,质数是“不可分割”的数。
100以内的质数表:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
(共25个)
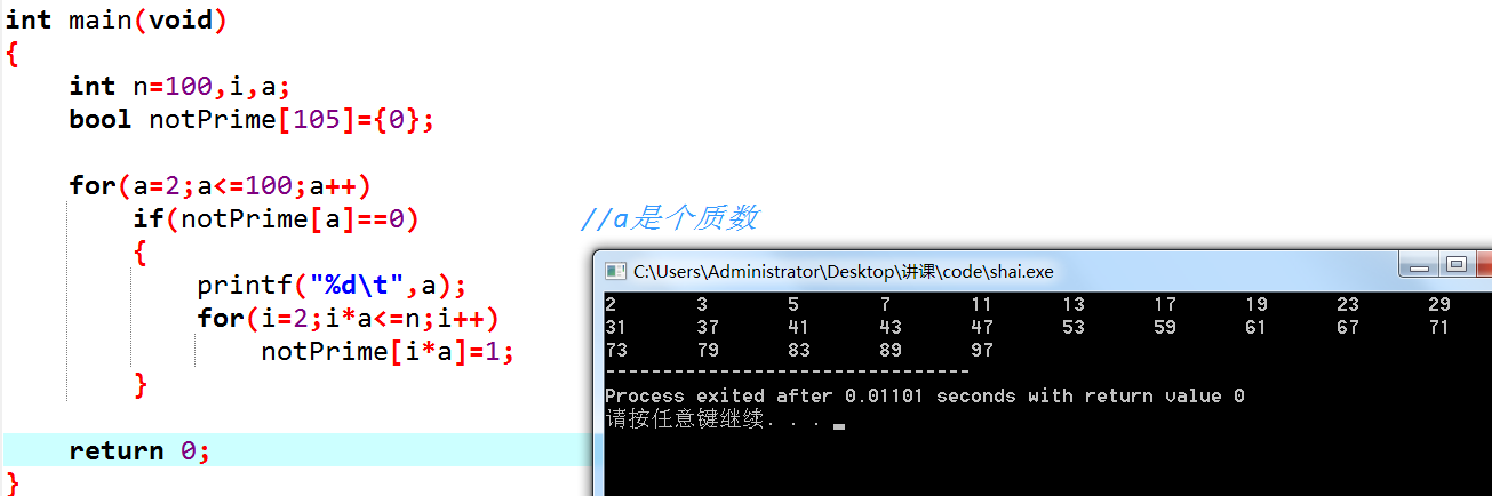
找质数:
筛法
首先,我们筛掉2的倍数,然后筛掉3的倍数,然后筛掉5的倍数……剩下来的数就是质数。



评论区